基于电化学阻抗谱与HO-TFRNN模型的磷酸铁锂电池SOC估计
作者:江屹峰 全惠敏 卢继武
单位:湖南大学
引用本文:江屹峰, 全惠敏, 卢继武. 基于电化学阻抗谱与HO-TFRNN模型的磷酸铁锂电池SOC估计[J]. 储能科学与技术, 2026, 15(1): 220-229.
DOI:10.19799/j.cnki.2095-4239.2025.0709
本文亮点:1.本课题采用等效电路模型与数据驱动相结合的方式,充分挖掘EIS数据的内在信息,从等效电路模型的众多参数和全频段EIS数据中优选与电池状态密切相关的参数特征子集,作为后续电池状态估计模型的输入,提高算法精度。2.目前基于EIS数据对锂离子电池状态估计的研究,常采用CNN、DNN等基础神经网络结构,本课题拟采用一种TFLSTM与多种新的算法结构如HO算法等相结合的估计模型用于磷酸铁锂电池的状态在线估计。
摘 要 准确估算锂电池的荷电状态(SOC)对提升电池系统性能与可靠性至关重要。由于传统估算方法在进行磷酸铁锂电池SOC估计时,往往存在精度不足、稳定性差等问题,为了提高对电池SOC估计的精度,本研究结合电化学阻抗谱(EIS)准确反映电池内部电化学状态的优势和混合时间-频率循环神经网络(TFRNN)强大的序列处理能力,提出了一种基于EIS和TFRNN的磷酸铁锂电池SOC估计算法。首先,本研究在25℃环境下测量并分析了商用18650磷酸铁锂电池在不同SOC下的EIS曲线,通过等效电路建模与频域分析相结合的方式提取特征参数,并最终选取了0.1 Hz处幅值与相位、100 Hz处实部与虚部等参数作为SOC估计的输入特征构建数据集。然后,本研究提出利用Transformer改进的TFRNN模型来估计电池SOC,同时引入河马仿生优化算法(HO)优化超参数以减少调参时间。利用自建的数据集进行实验验证,结果表明:该模型估算误差在3%以内,均方根误差为0.65050%,平均绝对误差为0.66734%,最大误差2.92306%。同时,本研究还采集了20℃和15℃的数据集进行对比验证,结果证明所提模型在多个数据集下都具有高度稳定性与精确性,能实现对磷酸铁锂电池SOC的精准估算。
关键词 锂离子电池;荷电状态;电化学阻抗谱
锂电池因其寿命长、环境友好等优点而被广泛应用于电子产品、电动汽车、储能装置、航空航天等领域。国内外锂电池产业链的逐步完善,电池材料与性能取得突破性进展使锂电池成本持续下降,推动市场规模不断扩大。其中,以磷酸铁锂为主要材料的新型锂电池表现尤为突出,在储能领域市场份额已超过90%。电池荷电状态(state of charge,SOC)表征电池的剩余容量,是电池状态估计中最重要的参数之一。准确估计电池SOC有助于优化电池使用管理,延长电池循环寿命,提升电池系统性能与可靠性等,因此实现电池SOC的准确估计是一个非常重要的问题。
现在主要的SOC估计方法有5种。①开路电压法(open-circuit voltage method,OCV),该方法在电池内部化学体系处于平衡状态时能近似估计实际的SOC状态,但是该方法需要电池保持长时间静置状态,不适用于实时估计。②安时积分法(Ampere-hour integration),该方法具有操作简单、计算成本低等优点。然而安时积分法本身无法准确确定电池的初始SOC值,因此无法避免引入较大的估计误差。③传统的模型驱动的估计方法,如扩展卡尔曼滤波法(Kalman filter,KF),能较准确估计多温度下的SOC状态,但该类方法复杂度高、估算耗时较长。④数据驱动的估计方法。使用深度学习方法样本对数据进行训练,能够建立起电池运行数据与实际电池状态之间的关系,从而估计电池状态。该类方法具备强大的非线性处理能力,能够避免建立高精度电池模型所带来的耗时过长问题,尤其适用于长期使用和动态工况下的估计。⑤基于电化学阻抗谱(electrochemical impedance spectroscopy,EIS)的方法。该方法可以非侵入式测试电池内部状态而且不需依赖电池的工作工况。EIS方法通过施加一定幅值且不同频率的交流(AC)信号,测量输出电压的幅值与相位,从而获取电池的电化学动态特性。EIS已成功应用于电池研究领域,包括对磷酸铁锂动力电池进行性能评估、电池状态监测、电极材料研究和电解质界面研究等。
基于深度学习和EIS的优势,研究者们近年来逐渐开始将之应用于电池SOC状态估计中。Messing等提出了一种基于深度神经网络(deep neural networks,DNN)和EIS的电池SOC估计策略,并验证其有效性;于天剑等提出了一种将自适应加权多通道长短期记忆网络(long short-term memory,LSTM)与Transformer融合的算法,以较高精度实现了对电池SOC和SOH的估计;陈金荣等在不同SOC条件下对三元锂电池进行了EIS测试,验证了EIS用于估计各种电池状态以及诊断电池故障的适用性,说明基于EIS的电池状态估计可扩展到三元锂离子电池等多种电池上;Pang等通过混合脉冲功率特性(HPPC)实验利用EIS数据建立二阶Thevenin等效电路模型,验证了EIS数据与SOC之间的强相关性。
现有研究表明基于EIS的方法会产生大量数据,若通过传统方法处理数据比较困难,而深度学习则需要大量的数据才能较好地分析出数据之间的关系。同时,将EIS数据结合等效电路模型提取其中的参数,将等效电路模型中的参数与EIS原始数据中的阻抗数据结合起来则可以更全面地利用EIS数据。因此,本研究将EIS与等效电路模型相结合获得特征数据,然后采用深度学习的方法进行电池SOC估计。首先通过大量实验采集了LFP电池在不同SOC状态下的原始EIS数据集;随后通过对EIS数据的处理,从等效电路模型参数和全频段EIS数据中筛选出与SOC相关性最强的特征参数子集,作为后续估计模型的输入;进而通过研究对比多种神经网络结构与优化算法,提出了基于河马优化算法(hippopotamus optimization,HO)和混合时间-频率循环神经网络(time-frequency recurrent neural network,TFRNN)的SOC估计算法。算法先采用TFRNN网络对电池SOC进行估计,确保算法的初始精度,然后引入Transformer对网络结构进行改进,再使用HO算法对算法中的各个超参数进行调优,提高了估计的精度。
1 电池测试系统与数据集构建
1.1电池测试系统搭建
为构建锂电池的数据集,本研究搭建了如图1所示的电池测试系统。该系统主要由恒温箱(温度调节)、电池测试仪BTS4000-5V30A(电池充放电)、电化学工作站CS310M(测试电化学阻抗谱)及上位机(数据处理)组成。其中充放电设备电压控制范围为25 mV~5 V,精度高达0.05%;电化学工作站电压控制范围为±10 V,电流控制范围为±2 A,电压分辨率为1 μV,电流分辨率为1 pA。利用图1所示系统,本研究对多个18650型商用锂离子电池进行了充放电实验和EIS测试,该电池充电截止电压为4.2 V,放电截止电压为2.75 V,容量为1500 mAh。

图1 电池测试系统
1.2SOC原始数据集采集
利用图1所示的电池测试系统,本研究采集了多组锂离子电池SOC的EIS原始数据。通过实验数据分析发现,当SOC以10%为间隔划分时,相邻SOC状态间的电池EIS数据差异较小,特征区分度不足。为提高特征参数表征能力并降低离散数据处理量,本研究采用20%的SOC间隔划分采集原始数据,使用了10%、30%、50%、70%、90%的数据进行研究,同时加入满电和空电量2个状态下的SOC数据,即最终选择0、10%、30%、50%、70%、90%、100%七个理论SOC点的数据进行后续处理。这些数据包括在每个SOC下利用多个磷酸铁锂电池进行的共1000余次循环中采集的不同频率的幅值相位以及阻抗的实部和虚部等信息。数据采集流程如下。
①恒温控制。使用恒温箱维持环境温度,电池测试前静置30 min确保内外温度均衡。
②充放电设置。采用1 C电流(1.5 A)进行充放电,恒流充电至4.2 V后转为恒压充电,截止电流0.05 A(将电池充电至初始SOC为100%)。
③放电测试。恒流放电6 min对应SOC降低10%,每次放电后静置10 min以消除极化效应。
④EIS测量。在选取的各个理论SOC点进行EIS测试,每次EIS测量前后均保持10 min静置期。数据采集的流程如图2所示。
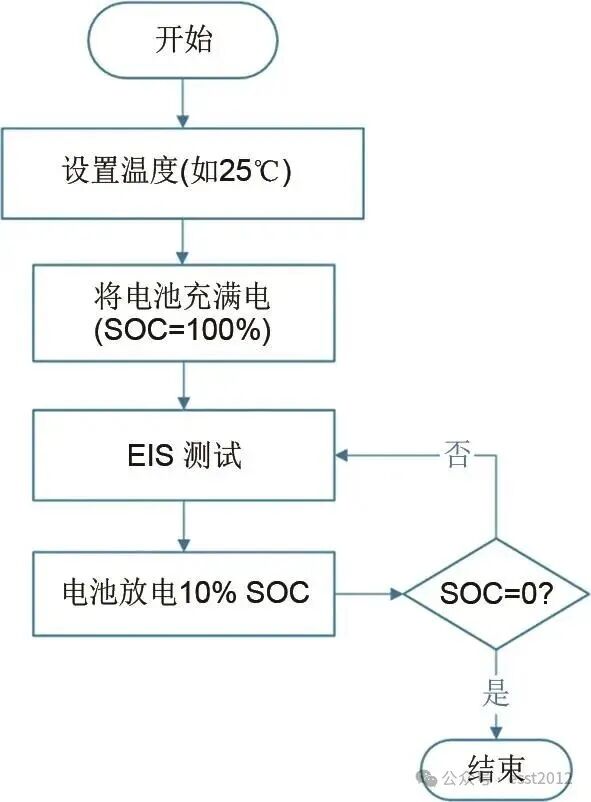
图2 SOC数据采集流程
1.3特征子集筛选
使用图1所示的测试系统,本研究收集了包含众多特征参数(如频率、阻抗、幅值和相位)的原始EIS数据。在这些参数中,部分特征可能是冗余或不相关的。过多的特征会导致估计模型对训练数据产生过拟合,进而降低其对未知数据的泛化能力。特征筛选通过有效剔除无关和冗余信息,构建与SOC相关性最高的特征子集,可以有效降低模型过拟合风险,提升模型性能和泛化能力。
为更完整地利用EIS数据中包含的信息,本研究结合等效电路建模与频域分析来选择特征子集。通过结合这两种方法,电池的动态特性得以全面表征。这确保了所选特征子集具有高度代表性,既有助于实现更精准的状态估计,也能推动构建具有通用性和适应性的状态估计模型。
1.3.1 等效电路模型构建
Westerhoff等基于锂离子电池的内部结构和电化学过程,提出一种综合等效电路模型。该模型包含四个关键组件:电阻R,代表电池各层内部的理想电阻。Warburg阻抗(W),表征与锂离子扩散相关的阻抗。电容C,反映电池中的理想电容行为。常相位元件(constant phase element,CPE),描述电池内部的非理想电容特性。Westerhoff提出的模型结构如图3所示。
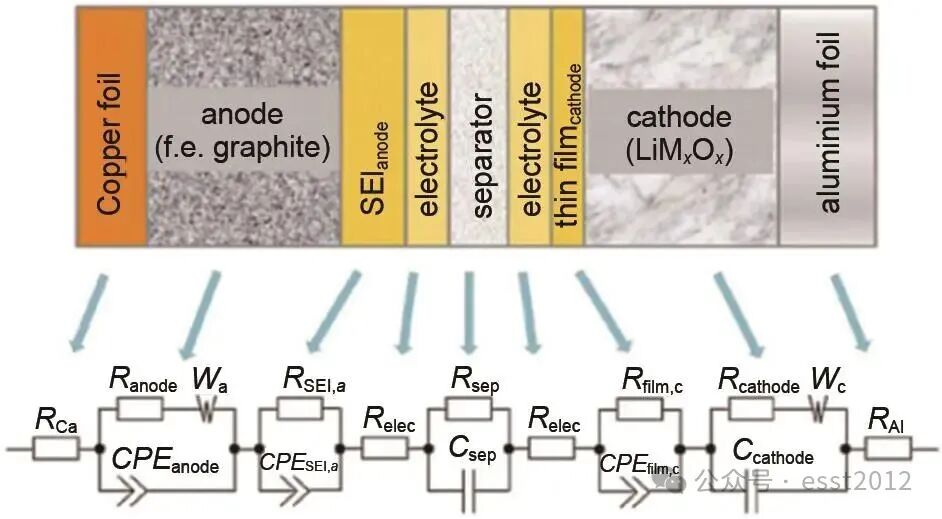
图3 Westerhoff提出的等效电路模型
尽管该模型全面刻画了电池系统,但其包含的变量较多,部分变量与电池SOC的关联性较弱。因此,在进行阻抗分析时,可根据需求对模型进行简化或修正,重点关注与电池SOC相关的变量。
根据频率特征,EIS曲线可分为三个区域。高频区因多孔电极结构及连接导线呈现感抗特性,半圆曲线与X轴交点的实部值对应欧姆电阻,一般包含电解液、隔膜和集流体的内阻。中频区的半圆一般认为与电池的电荷转移过程相关,此半圆一般用电荷转移内阻R和双电层电容C9并联的方式来体现。低频区表现为倾斜线,理论斜率为1,代表锂离子在电极中的扩散行为。该扩散过程由W描述,其中锂离子在电极材料颗粒内部的扩散系数是体现离子扩散动力学的关键参数,反映电极的高倍率放电能力。一个典型的电池EIS曲线如图4所示。
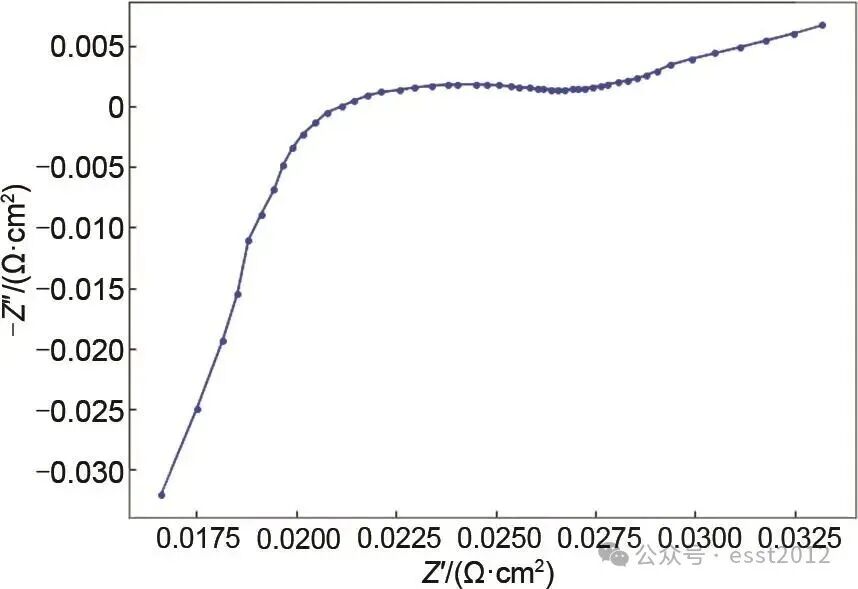
图 4 典型的EIS曲线图
通过对电化学阻抗谱的组成分析,可以将磷酸铁锂电池的等效电路模型简化为一个包含电感L1(L)、欧姆电阻R1(R)、电荷传递电阻R2和双电层电容CPE1并联(QR)以及韦伯阻抗W1(W)的电路。将这四部分元件串联起来即可初步建立磷酸铁锂电池的等效电路模型。使用Zsimpwin软件进行测试拟合,经过仿真多种等效电路模型对拟合结果进行对比,如LR(QR)(QR)W、LR(QR)W、LR(QR)(QR)等模型,本研究最终采取了LR(QR)(QR)W等效电路模型,其结构和拟合结果如图5所示。
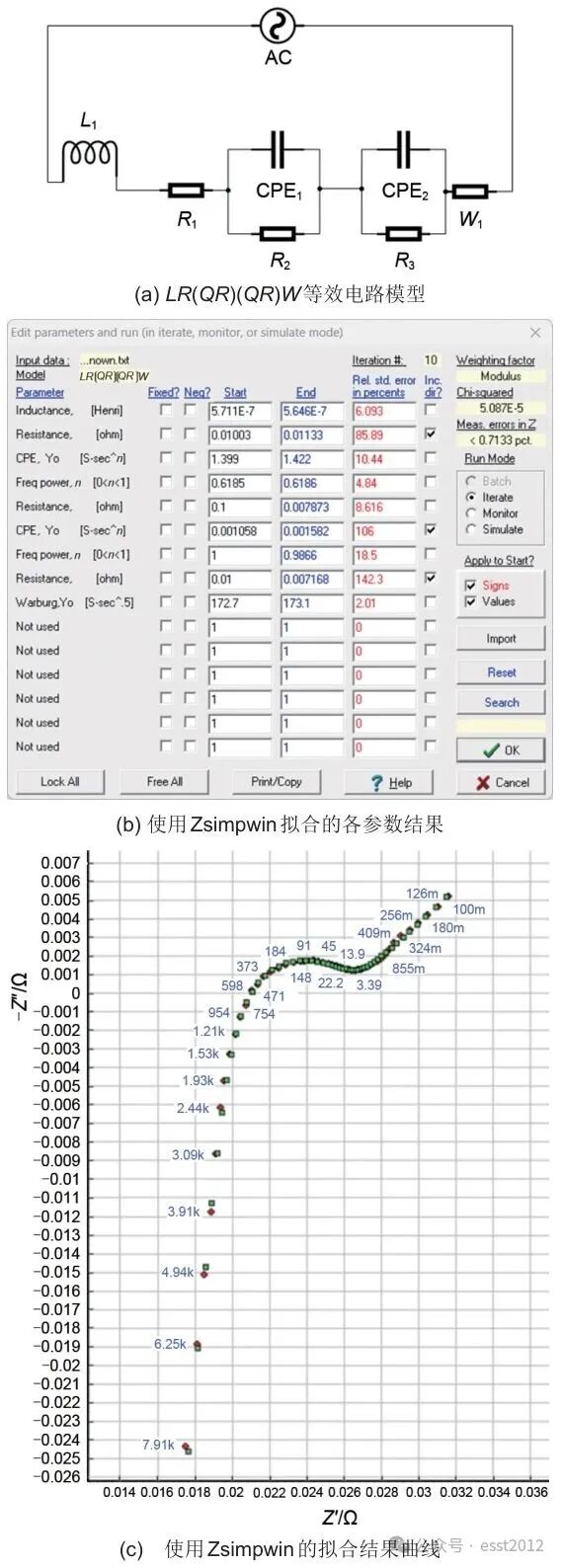
图5 等效电路模型及拟合结果
图5(b)给出了该电池等效电路模型的各参数的拟合误差,图5(c)为拟合结果曲线,其中红色点为原始数据点,绿色点为拟合的数据点。由拟合结果可看出,W阻抗的拟合误差最低,因此初步判断W可以作为一个特征参数提取出来,同时,本研究采取了皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,PPMCC)对该参数与电池SOC的相关性进行评估和验证。
采用PPMCC方法可以对等效电路模型中的各个参数和SOC的相关性进行评估,其中:当相关系数越接近1时,表示变量之间越正相关。当相关系数越接近-1时,表示变量之间越负相关。当相关系数为0时,表示两个变量之间没有线性关系。等效电路模型参数与SOC之间的皮尔逊相关系数热力图,如图6所示。从图可以看出W与SOC的相关系数为0.98,比其他参数与SOC的相关系数都大。
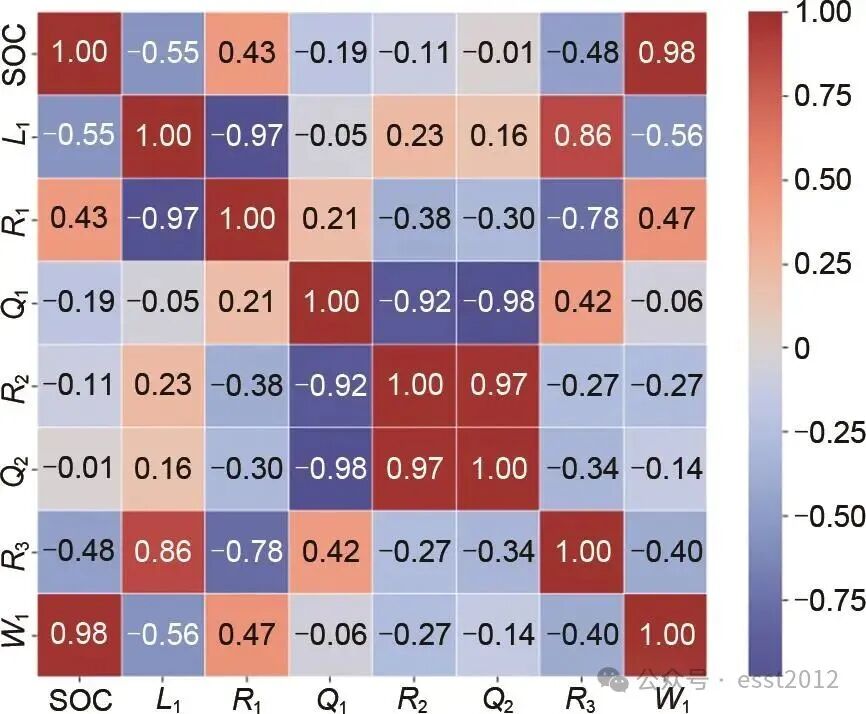
图 6 皮尔逊热力图
综上所述,W阻抗的拟合误差最小,同时与SOC的相关性最高,因此本研究选择了等效电路模型中的W阻抗作为一项特征参数。
1.3.2 SOC频域特征子集筛选
单独的W阻抗作为一个特征参数,不能完整地表征电池在不同SOC状态下的特征,因此还需要进一步建立能完整表征不同SOC下特征的参数集。本研究继续采用频域分析方法选取特征参数。通过分析1.2节中得到的电池在不同SOC值下的原始EIS数据,绘制出了如图7所示的电池奈奎斯特图(a)、幅频图(b)和相频图(c)。
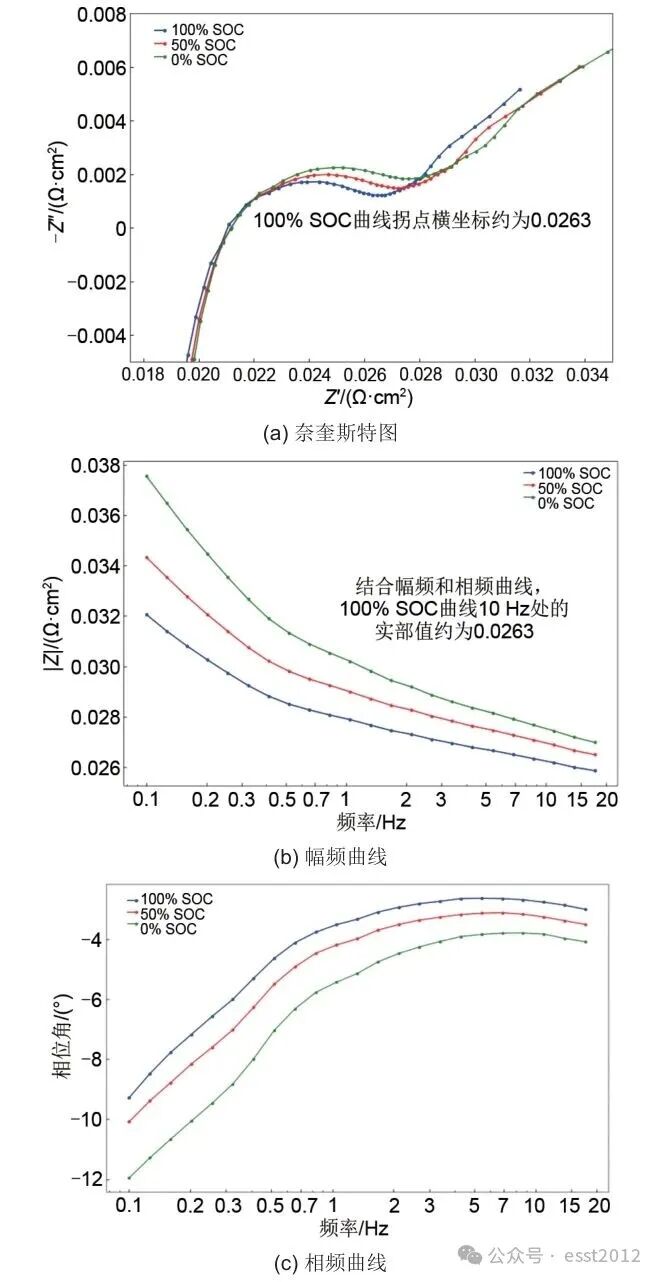
图7 25℃下不同SOC的EIS曲线
在图7(a)中半圆曲线和直线段的交会点通常对应EIS中的某些特征频率,这些特征频率与电池的内部动态行为密切相关。例如,半圆曲线的直径大小通常与电解质扩散过程的速率有关,而直线段的斜率通常与电极反应的动力学特性有关,半圆曲线与直线段的交会点同时包含了半圆曲线与直线段所代表的电池内部动态行为的共同信息。根据对图7(a)、(b)结合的分析,各SOC下的幅频曲线中,10 Hz附近的阻抗值恰好对应各自奈奎斯特图中半圆曲线与直线段的交会点处的阻抗,可见半圆曲线与直线段的交会点所表示的频率值会随着SOC的增大而减小。因此,可以选用该频率点(10 Hz)的阻抗值用于推断出电池的SOC变化。
根据图7(b)、(c)可以看出,0.1 Hz处的幅值和相位随着SOC的变化非常明显,这是因为在低频区域,电化学阻抗谱反映了电池内部的电化学反应动力学特性,而0.1 Hz处的幅值和相位可以提供关于电解质扩散过程的信息,这个过程与电池的SOC密切相关,因此,可以选用0.1 Hz处的幅值和相位用于磷酸铁锂电池SOC的估计。
2 基于EIS的电池SOC估计算法研究
因为所选多特征参数与电池SOC之间呈现非线性关系,鉴于人工神经网络在处理非线性问题方面的优势,本研究采用神经网络构建电池SOC估计模型,以建立这些特征参数与电池SOC之间的映射关系。
2.1基础网络选择
卷积神经网络(convolutional neural network,CNN)是一种深度学习模型,Zhang等比较了GPR,SVMs和CNN在SOC估计中的效果,发现CNN网络的误差最低。DNN是一种具有强大特征学习能力和非线性处理能力的计算模型。Messing等利用DNN网络提取多个特征参数与SOC之间的关系,并得到RMSE小于5%的预测结果。循环神经网络(recurrent neural network,RNN)是一种适合处理序列数据的神经网络。Yin等比较了CNN、RNN、LSTM等网络在SOC估计中的优缺点,总结出RNN在捕捉数据序列之间的关系上更有优势。TFRNN网络是一个由多个TFRNN块、全连接层和卷积层堆叠得到的网络,TFRNN块结构如图8所示。其核心工作方式是通过双向特征提取机制同时捕获信号的时域动态特性和频域结构特征,两个特征维度通过残差连接进行特征融合,并结合注意力机制自适应地加权重要特征。这种架构,相比传统RNN,能更好地处理更复杂的数据。Xie等提出了一个基于TFRNN块构建的TRLS框架在多尺度下分析医疗信号类型的时频序列数据,并通过多个该类数据集验证了其优势。
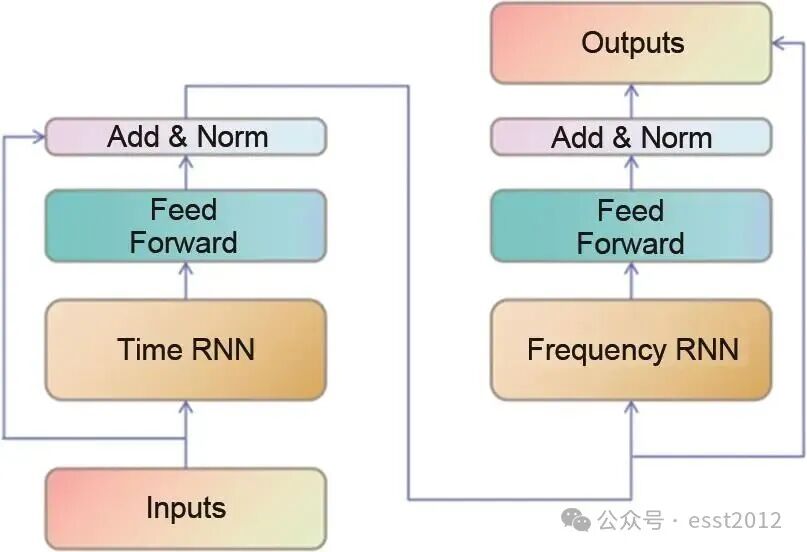
图 8 TFRNN块
本研究首先使用CNN、DNN、RNN、TFRNN网络来对SOC进行估计。在对这些不同神经网络的初步训练中均采用了相同的超参数设置(batch_size=8,epochs=80),性能对比共应用了三个估计指标:①均方根误差(RMSE),用于衡量模型预测值与实际值之间的平均差异;②平均绝对误差(MAE),用于衡量模型预测值与实际值之间的平均绝对差异;③最大误差(ME),用于表示衡量值和实际值之间的最大偏差。
仿真实验在自采集的同一SOC数据集上进行,得到的估计结果如表1所示。
表1 四种网络的估计结果指标 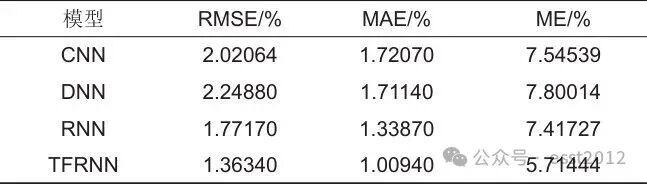
从表1中可以看到,TFRNN网络的估计结果的RMSE约为1.36340%,MAE约为1.00940%,ME约为5.71444%,这三项指标均优于其他网络的指标,表明该神经网络的综合估计效果更好,证明了基于TFRNN的网络模型对于实现电池状态估计的可行性。TFRNN网络的拟合结果如图9所示,可以看出TFRNN网络对SOC的估计效果较好,结果的最大误差均控制在6%以内,且大多数误差均在4%以内。
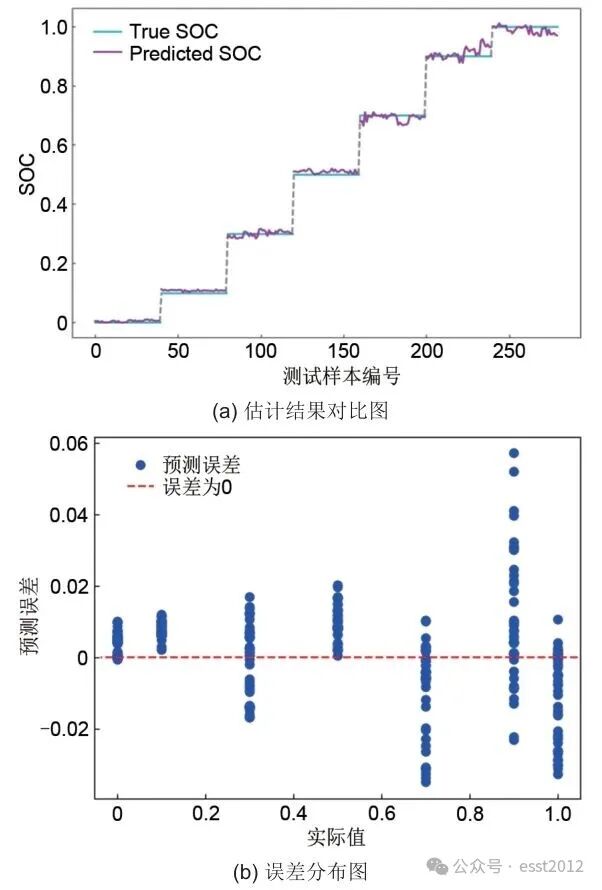
图 9 TFRNN模型的估计结果
2.2算法优化
2.2.1 HO算法
由于仅使用基础神经网络的估计算法得到的结果不够精确而且调参过程较长,为了提高算法的性能和调参效率,本研究将传统网络与仿生优化算法相结合来取得最优超参数。
仿生算法是一类基于自然界中生物行为的优化算法,常用来寻找复杂问题的最优解。目前主要的仿生算法有:粒子群算法(particle swarm optimization,PSO),蚁群算法(ant colony optimization,ACO),遗传算法(genetic algorithm,GA)等,但是上述算法在面对复杂连续数据时均有局限性。本研究采用的HO算法是一种基于河马群体行为的新型元启发式优化算法,灵感来自河马在自然环境中的社交、觅食和防御机制。该算法通过模拟河马的群体互动、领地意识和水陆活动来平衡全局探索与局部开发,适用于解决复杂优化问题,但是该算法作为一个新型算法,实验验证较少。在电池SOC估计中,数据较复杂,因此本研究选择引入新型的HO算法对算法进行优化,选出最优的神经网络的超参数组。
HO仿生优化算法核心原理和特点如下。①社会等级分层:河马群中存在明确的等级制度,主导个体将引导群体移动。在算法中,适应度最优的解即对应主导个体。②领地意识与局部开发:河马通过甩尾、吼叫等行为标记领地,避免冲突。算法中,这一行为被建模为在当前位置附近进行精细搜索,通过随机扰动当前解探索邻域,增强局部寻优能力。③群体迁移与全局探索:河马群体为寻找资源会集体迁移。算法中,主导个体的位置信息被用于引导其他个体向潜在最优区域移动,结合随机扰动避免陷入局部最优。④觅食行为:算法通过迭代周期动态调整搜索策略。早期大范围随机探索,提高多样性;后期小范围局部开发,加速收敛,以寻找最优解。⑤防御机制(多样性保持):当种群陷入停滞(如适应度长期未改进),随机生成新个体模拟外来入侵,打破局部最优。
实验中,HO算法的关键参数有:①种群大小(pop_size),代表每代河马(候选解)的数量。②迭代代数(num_generations),代表优化迭代的总轮数。③觅食行为参数,代表局部扰动幅度,用于探索附近解。④社交行为参数,代表向最优个体靠近的学习率。
经过实验对比,本研究最终选择的HO参数值如下:pop_size为10,num_generations为10,觅食行为参数为(0,0.1),社交行为学习率为0.5。
本研究引入HO算法优化的超参数组包含以下三个参数:隐藏单元(hidden_units),是神经网络中隐藏层(hidden layer)的神经元数量,隐藏单元越多,模型能学习更复杂的特征,但也可能增加过拟合风险;批大小(batch_size),表示每次训练时一次性输入模型的样本数量,影响训练速度和内存占用以及控制梯度更新的稳定性;丢弃率(dropout_rate),表示在训练过程中随机丢弃神经元的比例,用于防止神经元过度依赖特定特征,减轻过拟合。经过HO算法优化之后,最终得到的超参数组如下:hidden_units为93,batch_size为15,dropout_rate为0。
2.2.2 Transformer
Transformer是由Vaswani等提出的一种基于自注意力机制、用于自然语言处理的深度学习模型。其核心结构由编码器和解码器组成。编码器通过多头注意力机制和前馈神经网络层处理输入序列,捕捉全局依赖关系;解码器则结合编码器输出和掩码多头注意力,逐步生成目标序列。与传统的循环神经网络模型相比,Transformer能够并行计算,从而获得更快的训练速度,同时,Transformer在捕捉长序列的复杂数据的关系上更加有效。Ekambaram等将基于Transformer的模型应用于时间序列数据中并验证了其有效性。鉴于Transformer的诸多优势,本研究将Transformer块嵌入了TFRNN块中,对原模型进行改进。改进后的TFRNN块如图10所示。
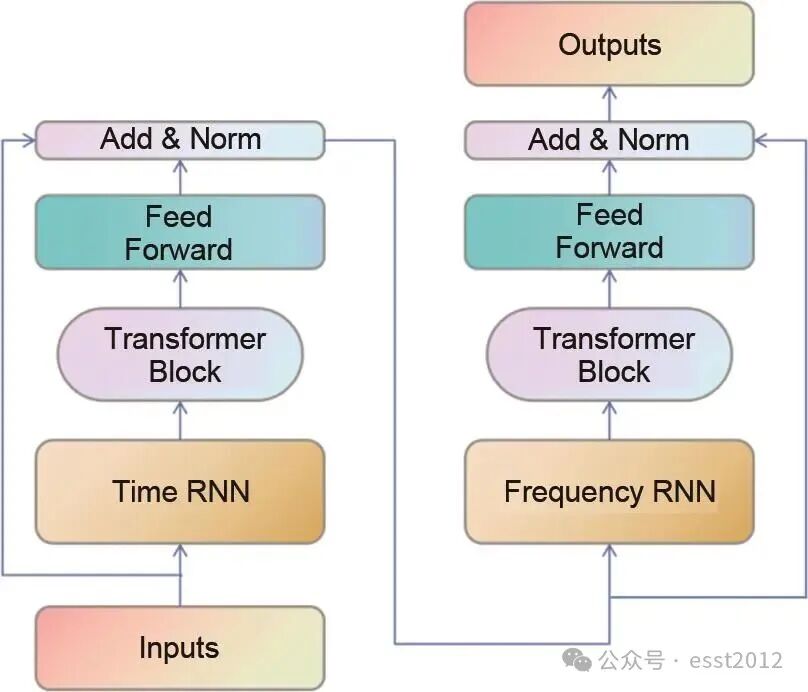
图 10 改进后的TFRNN块
2.3实验结果分析
引入HO优化算法和Transformer块改进后,使用2.1中使用的数据集进行训练验证,得到的结果如表2所示。
表2 各算法的估计结果指标 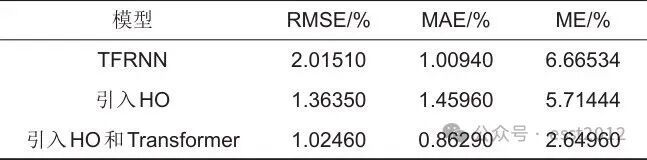
从表2中可知,在引入HO算法后,SOC估计结果的RMSE从2.01510%降到1.36350%,ME从6.66534%降到2.64960%。而在引入HO算法并进一步用Transformer改进TFRNN模型后,RMSE进一步降到1.02460%,MAE降到0.86290%,ME降到2.64960%。实验结果说明改进后模型较改进前各项指标均有明显提升。使用25℃下的SOC数据集得到的估计结果如图11所示,由图可以看出算法的估计误差全部控制在3%以内。实验结果表明,HO-TFRNN-Transformer算法在电池状态估算中展现出较高精度。
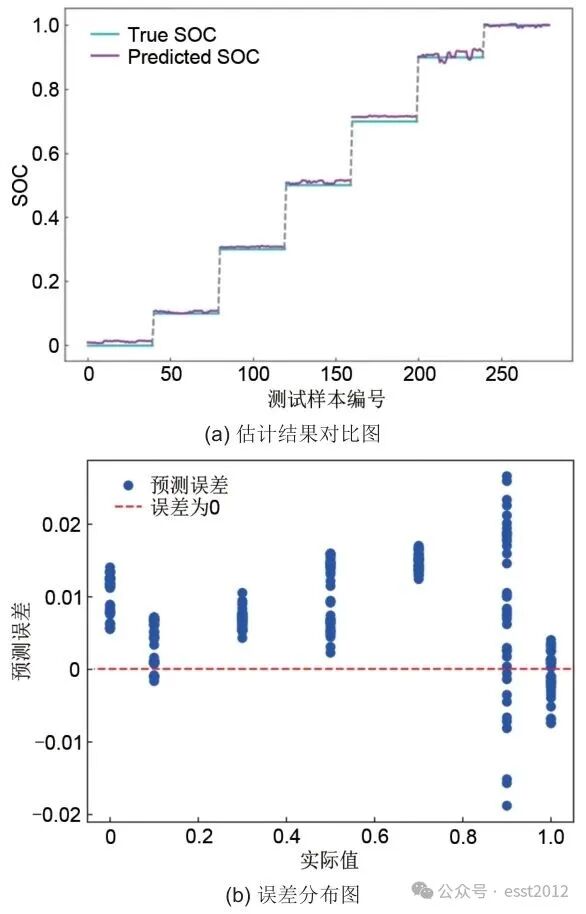
图11 HO-TFRNN-Transformer模型的估计结果
最后,本研究还使用了15、20℃下的SOC数据集进行验证,得到的指标如表3所示。由表3可知,15℃下采集的SOC数据集在HO-TFRNN-Transformer估计算法下,RMSE为1.03001%,MAE为0.87560%,ME为1.904332%,而20℃下采集的SOC数据集下RMSE为1.39880%,MAE为1.18690%,ME为2.84019%。同时,实验还使用了在25℃下约800次循环得到的数据集进行对比,得到的三项指标分别为0.65050%,0.66734%,2.92306%,与表2和表3其他数据集所得结果差别均不大,说明了该算法的稳定性。
表3 各个数据集的对比验证结果 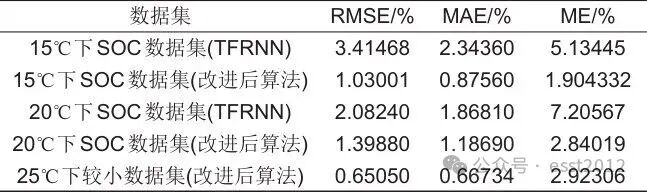
结合上述数据分析,本研究提出的算法在各个温度下的电池状态估计中均有较好的估计效果,是电池状态估计的有效方案。
3 结 论
为实现电池状态的精确估计,本研究用结合EIS频域分析与等效电路模型的方法获取数据集,然后提出基于改进TFRNN的SOC估计算法,并通过实验测试验证了该方法的有效性。
首先,在不同SOC状态下采集多组电池的EIS数据,利用等效电路模型和频域分析从原始EIS数据中提取关键特征参数,构成状态估计的特征子集。在此基础上,构建HO-TFRNN-Transformer模型以实现电池状态的精准估计。实验结果表明,与多种传统模型相比,本研究提出的HO-TFRNN-Transformer模型在各项误差指标上均有显著提升,比如在25℃的SOC数据集下,与传统RNN模型相比,估计结果的RMSE从1.77170%降至1.02460%,MAE从1.33870%降至0.86290%,ME从7.41727%降至2.64960%。这些数据表明HO-TFRNN-Transformer模型具有良好的数据拟合能力,能够精确估计电池状态。
综上所述,本研究提出的等效电路模型与频域分析相结合的方法,能有效筛选与SOC强相关的特征参数;而HO-TFRNN-Transformer算法进一步降低了估算误差,提升了模型的估计性能。因此,所提出的HO-TFRNN-Transformer算法为电池状态估算提供了高精度与高稳定性,在电池状态估算应用中具有实用价值。同时,研究表明基于EIS的电池状态估计策略可有效应用于三元锂电池等多种类的电池,因此在数据量足够的情况下,该估计模型还可扩展至三元锂电池等多种电池的SOC估计。
第一作者:江屹峰(2001—),男,硕士研究生,研究方向为锂离子电池状态估计;
通讯作者:全惠敏,副教授,研究方向为信号与信息处理 。
免责声明:本站所有信息均来源于互联网搜集,并不代表本站观点,本站不对其真实合法性负责。如有信息侵犯了您的权益,请告知,本站将立刻删除。